Solving Manning's equation for channels with Python

Manning's equation is a very common formula used in hydraulic engineering. It is an empirical formula that estimates the average velocity of open channel flow, based on a roughness coefficient.



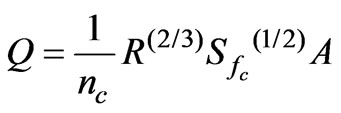
The problem of solving Manning's formula is that it is an implicit formula - the water depth variable (independent variable) is inside R (Hydraulic Radius) and A (flow area) - becoming dificult to isolate the independent variable.

A common approach for solving this equation is to use numerical methods, as the Newton-Raphson method.

In this case, we try different water depths until the function 

 - a manipulation of the original manning formula, became equal to zero.

An implementation for the resolution of the above, for open channels and using the Newton-Raphson approximation, is shown below.

If you found this code of this explanation useful, please let me know. 

def manningC(lam, args):
    Q,base,alt,talE,talD,nMann,decl = args
    area = ((((lam*talE)+(lam*talD)+base)+base)/2)*lam
    perM = base+(lam*(talE*talE+1)**0.5)+(lam*(talD*talD+1)**0.5)
    raio = area/ perM
    mannR = (Q*nMann/decl**0.5)-(area*raio**(2.0/3.0))
    return mannR

def solve(f, x0, h, args):
    lastX = x0
    nextX = lastX + 10* h  # "different than lastX so loop starts OK
    while (abs(lastX - nextX) > h):  # this is how you terminate the loop - note use of abs()
        newY = f(nextX,args)  # just for debug... see what happens
        # print out progress... again just debug
        print lastX," -> f(", nextX, ") = ", newY     
        lastX = nextX
        nextX = lastX - newY / derivative(f, lastX, h, args)  # update estimate using N-R
    return nextX

def derivative(f, x, h, args):
    return (f(x+h,args) - f(x-h,args)) / (2.0*h)

if __name__=='__main__':
    # arguments in this case are - flow, bottom width, height,
    # Left side slope, rigth side slope, manning, longitudinal slope
    args0 = [2.5,1,.5,1.0,1.0,.015,.005]
    initD = .01
    # call the solver with a precision of 0.001
    xFound = solve(manningC, initD, 0.001, args0)
    print 'Solution Found - Water depth = %.3f' %xFound