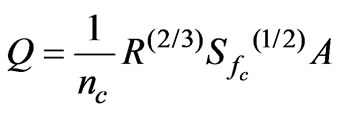A Library to connect Excel with Python - PYTHON FOR EXCEL

PYTHON FOR EXCEL. FREE & OPEN SOURCE.

xlwings - Make Excel Fly!

xlwings is a BSD-licensed Python library that makes it easy to call Python from Excel and vice versa:
Scripting: Automate/interact with Excel from Python using a syntax close to VBA.

- Macros: Replace VBA macros with clean and powerful Python code.
- UDFs: Write User Defined Functions (UDFs) in Python (Windows only).

Numpy arrays and Pandas Series/DataFrames are fully supported. xlwings-powered workbooks are easy to distribute and work on Windows and Mac.

Install with: pip install xlwings;

It is already included in Winpython and in Anaconda.

Links

https://www.xlwings.org/

http://docs.xlwings.org/en/stable/index.html

https://winpython.github.io/

https://www.continuum.io/downloads

Alternating Block Hyetograph Method with Python

To generate hypothetic storm events, we can use some methods as Alternating block method, Chicago method, Balanced method, SCS Storms among others.

In this post I show a way to generate a hypothetic storm event using the Alternating block method.

This python code uses the numpy library. The altblocks functions uses as input the idf parameters as list, and total duration, delta time and return period as floats.

import numpy as np

def altblocks(idf,dur,dt,RP):
    aDur = np.arange(dt,dur+dt,dt)    # in minutes
    aInt = (idf[0]*RP**idf[1])/((aDur+idf[2])**idf[3])  # idf equation - in mm/h
    aDeltaPmm = np.diff(np.append(0,np.multiply(aInt,aDur/60.0)))
    aOrd=np.append(np.arange(1,len(aDur)+1,2)[::-1],np.arange(2,len(aDur)+1,2))
    prec = np.asarray([aDeltaPmm[x-1] for x in aOrd])
    aAltBl = np.vstack((aDur,prec))
    return aAltBl

Make numpy array of 'datetime' between two dates

A simple way to create an array of dates (time series), between two dates:

We can use the numpy arange - https://docs.scipy.org/doc/numpy/reference/generated/numpy.arange.html , function which is most used to create arrays using start / stop / step arguments.

Syntax:
numpy.arange([start, ]stop, [step, ]dtype=None)

In case of datetime values, we need to specify the step value, and the correct type and unit of the timestep in the dtype argument

. dtype='datetime64[m]' will set the timestep unit to minutes;
. dtype='datetime64[h]' will set the timestep unit to hours;
. dtype='datetime64[D]' will set the timestep unit to days;
. dtype='datetime64[M]' will set the timestep unit to months;
. dtype='datetime64[Y]' will set the timestep unit to months;

For example:

import numpy as np

dates = np.arange('2017-06-01', '2017-06-02', 15, dtype='datetime64[m]')
# 15 is the timestep value, dtype='datetime64[m] means that the step is datetime minutes

This example will create an array of 96 values, between 01jun2017 and 02jun2017, with a time step of 15 minutes.

Solving Manning's equation for channels with Python

Manning's equation is a very common formula used in hydraulic engineering. It is an empirical formula that estimates the average velocity of open channel flow, based on a roughness coefficient.



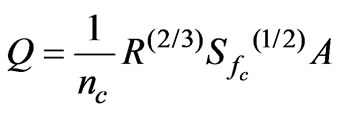The problem of solving Manning's formula is that it is an implicit formula - the water depth variable (independent variable) is inside R (Hydraulic Radius) and A (flow area) - becoming dificult to isolate the independent variable.

A common approach for solving this equation is to use numerical methods, as the Newton-Raphson method.

In this case, we try different water depths until the function 

 - a manipulation of the original manning formula, became equal to zero.

An implementation for the resolution of the above, for open channels and using the Newton-Raphson approximation, is shown below.

If you found this code of this explanation useful, please let me know. 

def manningC(lam, args):
    Q,base,alt,talE,talD,nMann,decl = args
    area = ((((lam*talE)+(lam*talD)+base)+base)/2)*lam
    perM = base+(lam*(talE*talE+1)**0.5)+(lam*(talD*talD+1)**0.5)
    raio = area/ perM
    mannR = (Q*nMann/decl**0.5)-(area*raio**(2.0/3.0))
    return mannR

def solve(f, x0, h, args):
    lastX = x0
    nextX = lastX + 10* h  # "different than lastX so loop starts OK
    while (abs(lastX - nextX) > h):  # this is how you terminate the loop - note use of abs()
        newY = f(nextX,args)  # just for debug... see what happens
        # print out progress... again just debug
        print lastX," -> f(", nextX, ") = ", newY     
        lastX = nextX
        nextX = lastX - newY / derivative(f, lastX, h, args)  # update estimate using N-R
    return nextX

def derivative(f, x, h, args):
    return (f(x+h,args) - f(x-h,args)) / (2.0*h)

if __name__=='__main__':
    # arguments in this case are - flow, bottom width, height,
    # Left side slope, rigth side slope, manning, longitudinal slope
    args0 = [2.5,1,.5,1.0,1.0,.015,.005]
    initD = .01
    # call the solver with a precision of 0.001
    xFound = solve(manningC, initD, 0.001, args0)
    print 'Solution Found - Water depth = %.3f' %xFound